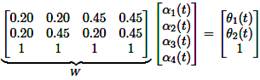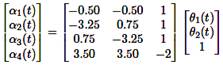|
Scientific Paper / Artículo Científico |
|
|
|
|
https://doi.org/10.17163/ings.n33.2025.02 |
|
|
|
pISSN: 1390-650X / eISSN: 1390-860X |
|
|
LIQUID LEVEL TRACKING FOR A COUPLED TANK SYSTEM USING QUASI–LPV CONTROL |
||
|
SEGUIMIENTO DEL NIVEL DE LÍQUIDO DE UN SISTEMA DE TANQUES ACOPLADO EMPLEANDO CONTROL CUASI-LPV |
||
|
Received: 13-03-2024, Received after review: 21-05-2024, Accepted:
03-07-2024, Published: 01-01-2025 |
|
Abstract |
Resumen |
|
This article proposes
a gain-scheduling procedure based on quasi-LPV modeling for a nonlinear
coupled tank system to track the liquid level with zero steadystate
error. The nonlinearities are directly represented by a parameter vector that
varies within a bounded set constrained by the
physical limits of the tank system levels. This approach enables accurate
nonlinear system modeling using a linear parameter-varying model.
State-feedback linear controllers are designed at the extreme vertices of the
bounded set. The global controller is derived as the
weighted average of local controller contributions, with the weighting
determined by the instantaneous values of the parameter vector. Two
interpolation mechanisms are proposed to implement this weighted averaging of
the linear controllers. The results confirm the effectiveness of the proposed
method in achieving accurate liquid level trackin. |
En este artículo se propone un procedimiento de programación de ganancias basado en un modelado cuasi-LPV de un sistema no lineal de tanques acoplados para seguir el nivel de líquido con error en estado estacionario nulo. Las no linealidades están representadas directamente por un vector de parámetros que varía dentro de un conjunto acotado por los límites físicos del nivel del sistema de tanques. Esto permite un modelado exacto del sistema no lineal utilizando un modelo lineal de parámetros variantes. Luego, se diseñan controladores lineales de realimentación de estado en los vértices extremos del conjunto acotado. El controlador global corresponde a un promedio ponderado de las contribuciones locales. Esta ponderación depende de los valores instantáneos del vector de parámetros. Para implementar el promedio ponderado de los controladores lineales, se proponen dos mecanismos de interpolación. Los resultados obtenidos muestran la efectividad del método. |
|
Keywords: Coupled-Tank System, Gain
Scheduling, Nonlinear Systems, Quasi-LPV, Tracking Problem |
Palabras clave: sistema de tanques acoplados, programación de ganancias, sistemas no lineales, cuasi- LPV, problema de seguimiento |
|
1,*Departamento de Gestión de Proyectos y Sistemas, Universidad Metropolitana, Caracas, Venezuela. Corresponding
author ✉: pteppa@unimet.edu.ve. Suggested
citation: Teppa-Garrán, P.; Muñoz-de Escalona, D.
and Zambrano, J. “Liquid level tracking for a coupled tank system using
quasi–lpv control,” Ingenius,
Revista de Ciencia y Tecnología,
N.◦ 33, pp. 15-26, 2025, doi: https://doi.org/10.17163/ings.n33.2025.02. |
|
1. Introduction The control of liquid levels in
tanks is widely employed in various industries, including food and beverage
production, nuclear and petrochemical plants, and the pharmaceutical sector.
Generally, interactions between tanks occur due to coupling, resulting in
nonlinear behavior [1]. Numerous control strategies have been proposed for
coupled tank systems, including Proportional-Integral-Derivative (PID)
controllers [2–4], Fuzzy control [5,6], Model Predictive Control [7,8],
Backstepping Control [9,10], Sliding-Mode Control [11,12], Fractional PID
controllers [13, 14], Robust control [15]. Active Disturbance Rejection
Control [16,17] and Two-Degree-Of-Freedom controllers [18]. Some of these
techniques rely on nonlinear system theory, which can be challenging to
implement, while others employ linearization of the system equations around
an operating point.For the
local operating range, designs based on Jacobian linearization perform effectively. However,
under significant disturbances or when faster settling times are required,
the performance of such controllers can deteriorate due to a loss of
robustness. Gain scheduling [19, 20] is a
widely adopted approach in industry for controlling nonlinear systems by
breaking down the nonlinear design problem into several smaller, manageable
subproblems where linear design tools can be applied. For instance, in robot
control, controller dynamics are adjusted in real-time based on varying
inertia and geometry. Similarly, most aircraft control laws are modified by
interpolating individually designed controllers. In recent decades, the
Linear Parameter Varying (LPV) system theory has gained prominence as a
powerful paradigm for system identification, analysis, and controller
synthesis [21–23]. This class of systems is particularly valuable as it
allows nonlinearities to be incorporated as varying parameters within a bounded
set, ensuring that the possible trajectories of the LPV system encompass all
trajectories of the original nonlinear system. When these parameters include
state vector elements, the system is referred to as quasi-LPV [24]. In this
study, the nonlinearities of the tank system model, represented by liquid
levels, are considered uncertain but constrained within the technological
limits of the equipment ([0, 30]cm). This allows for an accurate
representation of the nonlinear terms by embedding them into a quasi-LPV
model. The advantage of this approach is that it enables the design of linear
controllers using state-space techniques, ensuring zero steady-state tracking
error for constant reference inputs and guaranteeing a pole-dominant
criterion [25, 26]. Within a gain-scheduling scheme,
the control of the nonlinear coupled tank system is achieved through local
controller interpolation. Two interpolation mechanisms |
are proposed: (1) analytical
interpolation, where a system of linear equations is continuously solved to
compute the weighting factors, and (2) geometric interpolation, where the
weights of the local controllers are determined based on the Euclidean distance
to some vertex points. Analytical interpolation, initially presented in [27]
and inspired by concepts from Takagi-Sugeno fuzzy
models, is implemented in this study in a simplified form without
incorporating any fuzzy elements. Geometric interpolation, on the other hand,
offers an innovative approach in this context. While quasi-LPV theory has
been widely applied in fields such as missile guidance [28, 29] and robotics
[30, 31], its application to tank systems remains relatively unexplored
despite the significant industrial relevance of this process. The results confirm
the effectiveness of the proposed method in controlling the coupled tank
system. The article is structured as follows: Section 2 details the quasi-LPV
control design method, with a particular focus on the formulation of two
interpolation mechanisms, which are integrated within a gain-scheduled
tracking control strategy and describes the coupled tank system’s nonlinear
model. In Section 3, the quasi-LPV design method is applied to the system.
Finally, the conclusions are presented in Section 4. Notation: Bold capital letters denote matrices, while
bold lowercase letters represent vectors (i.e.
2. Materials and methods 2.1.Quasi-LPV
control design Most existing nonlinear controller
synthesis approaches focus on input-affine systems [32], which are typically
described as equation (1):
Where x The first step in the synthesis
procedure is to derive a quasi-LPV representation of the form as seen in the
equation (2): |
For the nonlinear system described
in equation (1). Here
2.2. Interpolation mechanisms Defining
For each local model, a state
vector gain Ki can be designed. The parameter vector θ(t)
is then used to construct the overall gain-scheduled controller by
interpolating the local controllers. At any given time, θ(t) can
be expressed as equation (4):
The weights αi(t) are computed by solving the system of linear
equations:
Where:
The interpolation scheme based on
the weights computed from the continuous solution of equation (5) is referred
to as analytical interpolation to distinguish it from geometric
interpolation, which will be described below. At any given time, the Euclidean
distance between the state-dependent parameter vector |
The relative contribution of the
parameter vector
Points further from the vertices
should have lower weights. Therefore, the complementary distance,
As in the analytical procedure,
the weights computed using the geometric approach continuously satisfy the
equation 2.3.Tracking a step reference input Using
the computed weights, the model in equation (2) can be approximated as a
combination of the local linear models:
The design problem now focuses on
tracking a step reference input r(t) with zero steady-state error e(t)
defined as:
Where is the controlled output.
Taking the time derivative of equation (9), for a constant reference input
yields: |
Taking the time derivative of each local
linear model
Equations (11) and (12) can be combined as:
Where:
A state feedback gain for system (13) is
constructed as:
After integrating equation (14), the actual
control signal becomes:
Using the same weights , a time-varying state feedback gain
for system (8) is constructed as:
Where: Figure 1 illustrates the implementation of
the control policy described in equation (15) for each local model, as
defined in equation (3). Additionally, Figure 2 depicts the global controller
that enables the implementation of the control law in equation (16) by
interpolating the local |
controllers, either using weights computed
analytically (equation 5) or geometrically (equation (7)). For the augmented
tracking system in equation (13), the gain
Figure 1. Local tracking control system block diagram
Figure 2. Overall tracking controller implementation
by interpolating local controllers Where P represents the desired closed-loop
poles, selected to satisfy a guaranteed pole-dominant criterion [25, 26],
based on closed-loop design requirements specified in the time domain, such
as overshoot (OS) and settling time (Ts). In light of
the above discussion, the design algorithm for implementing the interpolated
control law in equation (16) is summarized in Table 1. Table 1. Design algorithm for quasi-LPV
control
|
|
2.4.Coupled Tank
System Figure 3 depicts the coupled tank system. It
consists of a single pump and two tanks, each equipped with a pressure sensor
to measure the water level. The pump transfers water from the bottom
reservoir to the top of the system. Depending on the configuration of the
outflow valves, water can flow into the upper tank, the lower tank, or both.
This configuration is illustrated in Figure 4, where the pump output is
connected to the first tank. x1 and x2 represent the water
levels in tanks 1 and 2, respectively. The vector functions in the form of
equation (18) for the coupled tank system are derived using Bernoulli’s law
and the mass balance principle [34] and are expressed as:
Figure 3. Coupled tank system
Figure 4. Standard configuration of the coupled tank
system |
Where A1 and A2 denote the
cross-sectional areas of tanks 1 and 2, respectively. Ad1,Ad2
represent the cross-sectional areas of the corresponding orifices, g is the
acceleration on Earth due to gravity, and Kf is the
pump flow constant. The numerical values of these parameters are provided in
Table 2. Table 2. Physical parameters of the coupled tank
system
3. Results and discussion This section outlines the implementation and
evaluates the performance of the quasi-LPV control method, as summarized in
Table 1. 3.1. Quasi-LPV model The input voltage applied to the pump serves
as the control signal, while the water level in the second tank is selected
as the controlled output. Based on equation (18), the nonlinear model of the
tank system can be expressed as:
The nonlinear terms in each equation can be
reformulated as follows:
Resulting in: |
Defining
the parameter vector in (19) as:
Utilizing the numerical values from Table 2,
the quasi-LPV model in the form of equation (2) is expressed as:
The liquid levels in the tanks are considered
uncertain but vary within their physical limits, as specified in Table 2,
over the interval:
When the liquid levels in the tanks vary
within the range specified in equation (22), the parameter vector in equation
(20) will fluctuate within the rectangular bounding box:
3.2.Local linearized
models The extreme parameter combinations within the
bounding box in equation (23) yield the following vectors:
|
This results in the following set of local
linearized models:
3.3.Local controllers Using equation (25), the augmented systems in
equation (13) for each vertex are given by:
The four controller gains
The resulting dominant poles are
3.4.Interpolation
mechanisms In the analytical approach, equation (5) is
represented as the following system of linear equations: |
|
Solving this system using the pseudoinverse
matrix
For geometric interpolation, equation (7) is
implemented directly using a Matlab function block.
A straightforward Matlab function code is written
and integrated into a Simulink model, which executes the simulation. 3.5.Gain-scheduled
control implementation The gain-scheduled control strategy depicted
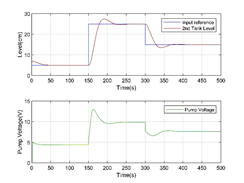
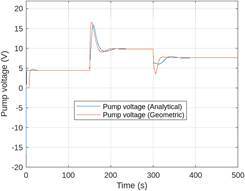
in Figure 2 was implemented. Figure 5 illustrates the liquid level response
in the second tank following a set-point change, comparing both interpolation
methods for the computed linear controllers (27).
Figure 5. Second tank closed-loop liquid level
response for analytical and geometric interpolation methods The geometric method encounters specific
issues at the start of the simulation due to its inability to provide the
required negative control action. After this initial phase, the performance
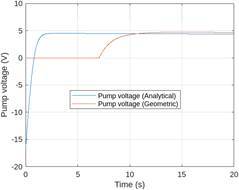
of both interpolation schemes becomes comparable. Figure 6 illustrates the control signal,
while Figure 7 focuses on the first 20 seconds of the control signal. It is
evident that when a negative control signal is required, the geometric scheme
remains at zero, confirming the issues observed at the beginning of the
simulation, as |
depicted in Figure 5. It is important to note
that the control signal provided by the pump cannot be negative, a limitation
not accounted for during the simulation when evaluating the performance of
both interpolation schemes.
Figure 6. Pump voltage control signal for analytical
and geometric interpolation methods
Figure 7. Detail of the control signal during the
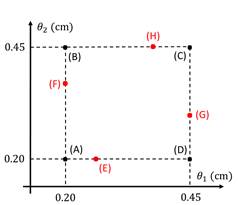
first 20 s 3.6.Further results Figure 8 illustrates the parametric bounding
box defined by equation (23). The previous results involved the
implementation of the gain scheduled controller through the interpolation
both geometric and analytical of the local controllers computed at the vertices
(A), (B), (C), and (D), based on a dominant pole criterion for the desiredOS and Ts specifications. Additionally, the
simulation permitted the control signal to take on negative values to
facilitate a comparison between the two interpolation mechanisms. The gain-scheduled controller is
implemented in this section, using various local controllers computed within
the region shown in Figure 8, as specified in Table 3. The control signal is
constrained to remain within the operational range of the pump (0-22 V), and
the desired closed-loop poles in equation (17) are selected as |
|
Figure 8. Points chosen in the parametric bounding box
(23) to compute local controllers Table 3. Points chosen in region (3) to compute local
controllers.
Model M1 utilizes the vertices of
the region, M2 computes the local controllers along the edges, and model M3
considers the extreme vertices of the region, where parameters θ1 and
θ2 take their minimum and maximum possible values. The selection of the
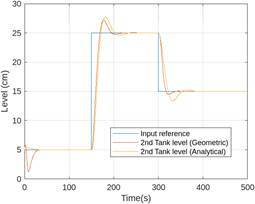
M3 model is justified by the well-known Edge Theorem [36]. Figure 9
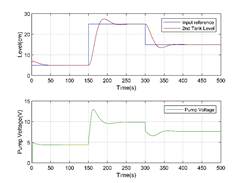
illustrates the level in the second tank and the pump control signal using
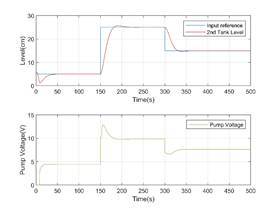
the M1 model with analytical interpolation.
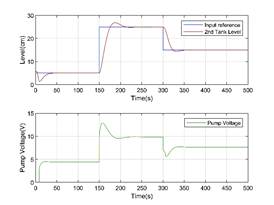
Figure 9. Second tank level and pump voltage for M1
model and analytical interpolation Figure 10 presents a similar
scenario employing geometric interpolation. Figures 11 ,
12 replicate the analysis for the M2 model, using analytical and geometric
interpolation mechanisms, respectively. |
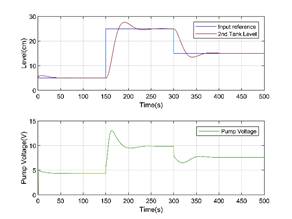
Figure 10. Second tank level and pump voltage for M1
model and geometric interpolation
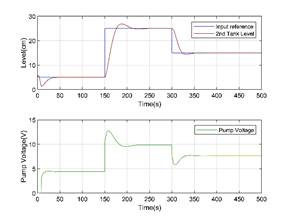
Figure 11. Second tank level and pump voltage for M2
model and analytical interpolation
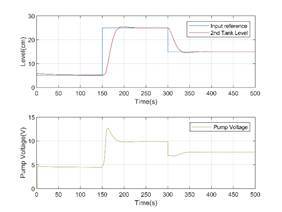
Figure 12. Second tank level and pump voltage for M2
model and geometric interpolation Figures 13 and 14 display the results for the
M3 model, again using analytical and geometric interpolation, respectively.
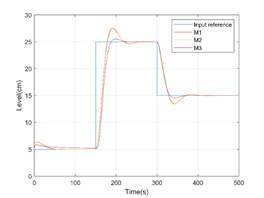
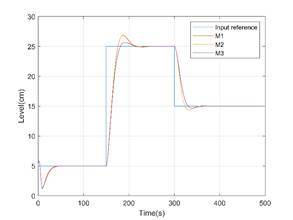
Finally, Figures 15 and 16 compare the evolution of the liquid level in the
second tank for all three models, with analytical and geometric interpolation
considered, respectively. |
|
Figure 13. Second tank level and pump voltage for M3
model and analytical interpolation
Figure 14. Second tank level and pump voltage for M3
model and geometric interpolation
Figure 15. Second tank level for models M1, M2 and M3
using analytical interpolation
Figure 16. Second tank level for models M1, M2 and M3
using geometric interpolation |
4.
Conclusions A gain-scheduled procedure was proposed to
control a coupled tank system modeled as a quasi-LPV system. The
nonlinearities of the model are directly captured by a set of uncertain
parameters that vary within a bounded set,
constrained by the physical limits of the tank system. Extreme combinations
of the parameter vector were computed, and local linear approximations were
obtained. These approximations were then used in the state-space synthesis of
control laws to track a constant reference input. The global controller was
constructed as a weighted average of the local contributions, where the
weights depended on the instantaneous values of the parameter vector. Two
interpolation mechanisms, geometric and analytical, were employed to
determine the weighted average of the linear controllers. The geometric
method is based on the Euclidean distance between the parameter vector and
the vertices, while the analytical method involves solving a linear system of
equations using the pseudoinverse of a matrix. The geometric scheme is
simpler and generates only positive control actions, with a very short
computation time. In contrast, the analytical scheme can provide both
positive and negative control actions but requires significantly more
processing time. Simulation results demonstrated that using the two extreme
vertices (Model M3) to compute the interpolated local controllers reduces the
computational effort needed. The primary limitation of the
methodology is the challenge of accurately determining the quasi-LPV model to
capture the system’s nonlinearities, which is not an easy task for all
plants. This indicates that the proposed approach may not be universally applicable.
However, when a nonlinear plant can be effectively modeled using a linear
parameter-varying system, the method is straightforward to implement and
yields satisfactory results. Another key aspect of the method is that the
control law for designing the local controllers is not limited to closed-loop
pole assignment, as demonstrated in this article. Various state-feedback
control strategies can be employed, including those that account for
optimality, robustness, and constraints. Additionally, although the
guaranteed pole-dominant criterion is suitable for linear systems, a notable
discrepancy emerged between the design specifications and the actual
performance in the case of the nonlinear tank system. This gap was mitigated
by setting dominant real poles to improve control over the output. Ongoing work focuses on the
real-time implementation of the proposed design method and the inclusion of
state observers. Acknowledgements The authors gratefully acknowledge the
support provided by the Research Program of the Metropolitan University in
Caracas, Venezuela, under project number PG-A-13-21-22. |
|
References [1] R. Grygiel, R. Bieda, and M. Blachuta,
“On significance of second-order dynamics for coupled tanks systems,” in 2016
21st International Conference on Methods and Models in Automation and
Robotics (MMAR), 2016, pp. 1016–1021. [Online]. Available:
https://doi.org/10.1109/MMAR.2016.7575277 [2] S. K. Singh, N. Katal, and S. G. Modani, “Multi objective
optimization of pid controller for coupled-tank
liquid-level control system using genetic algorithm,” in Proceedings of the
Second International Conference on Soft Computing for Problem Solving (SocProS 2012), December 28-30, 2012, B. V. Babu, A.
Nagar, K. Deep, M. Pant, J. C. Bansal, K. Ray, and U. Gupta, Eds. New Delhi:
Springer India, 2014, pp. 59–66. [Online]. Available:
https://doi.org/10.1007/978-81-322-1602-5_7 [3] D. L. Mute, S. R. Mahapatro, and K. K.
Chaudhari, “Internal model based pi controller
design for the coupled tank system: An experimental study,” in 2016 IEEE
First International Conference on Control, Measurement and Instrumentation
(CMI), 2016, pp. 72–76. [Online]. Available:
https://doi.org/10.1109/CMI.2016.7413713 [4] M. G. Stohy, H. S. Abbas, A.-H. M.
El-Sayed, and A. G. Abo El-maged, “Parameter
estimation and pi control for a water coupled tank system,” Journal of
Advanced Engineering Trends, vol. 38, no. 2, pp. 147–159, 2020. [Online].
Available: https://doi.org/10.21608/jaet.2020.73062 [5] L. Liang, “The application of fuzzy pid
controller in coupled-tank liquid-level control system,” in 2011
International Conference on Electronics, Communications and Control (ICECC),
2011, pp. 2894–2897. [Online]. Available:
https://doi.org/10.1109/ICECC.2011.6067785 [6] A. Başçi and A. Derdiyok,
“Implementation of an adaptive fuzzy compensator for coupled tank liquid
level control system,” Measurement, vol. 91, pp. 12–18, 2016. [Online].
Available: https://doi.org/10.1016/j.measurement.2016.05.026 [7] M. Essahafi, “Model predictive control
(MPC) applied to coupled tank liquid level system,” CoRR,
vol. abs/1404.1498, 2014. [Online]. Available:
https://doi.org/10.48550/arXiv.1404.1498 [8] J. Berberich, J. Köhler, M. A. Müller,
and F. Allgöwer, “Data-driven model predictive
control: closed-loop guarantees and experimental results,” at - Automatisierungstechnik, vol. 69, no. 7, pp. 608–618,
Jun. 2021. [Online]. Available: http://dx.doi.org/10.1515/auto-2021-0024 |
[9] J. Jiffy Anna, N. E. Jaffar, and F. Riya
Mary, “Modelling and control of coupled tank liquid level system using
backstepping method,” International Journal of Engineering Research and
Technology, vol. 4, no. 6, pp. 667–671, 2015. [Online]. Available:
http://dx.doi.org/10.17577/IJERTV4IS060710 [10] J. Dai, B. Ren, and Q.-C. Zhong,
“Uncertainty and disturbance estimator-based backstepping control for
nonlinear systems with mismatched uncertainties and disturbances,” Journal of
Dynamic Systems, Measurement, and Control, vol. 140, no. 12, Jul 2018,
121005. [Online]. Available: https://doi.org/10.1115/1.4040590 [11] F.
Abu Khadra and J. Abu Qudeiri, “Second order
sliding mode control of the coupled tanks system,” Mathematical Problems in
Engineering, vol. 2015, no. 1, p. 167852, 2015. [Online]. Available:
https://doi.org/10.1155/2015/167852 [12] K. K. Ayten and A. Dumlu, “Implementation of a pid type sliding-mode controller design based on
fractional order calculus for industrial process system,” Elektronika
ir Elektrotechnika, vol.
27, no. 6, pp. 4–10, Dec. 2021. [Online]. Available:
https://doi.org/10.5755/j02.eie.30306 [13] M. Vashishth, L. S. Rai, and A. V. R. Kumar, “Liquid level
control of coupled tank system using fractional pid
controller,” 2013. [Online]. Available: https://upsalesiana.ec/ing33ar2r13 [14] P. Roy and B. Krishna Roy, “Fractional order pi control applied
to level control in coupled two tank mimo system
with experimental validation,” Control Engineering Practice, vol. 48, pp.
119–135, 2016. [Online]. Available:
https://doi.org/10.1016/j.conengprac.2016.01.002 [15] M. H. Jali, A. Ibrahim, R. Ghazali, C. C. Soon, and A. R. Muhammad, “Robust Control Approach of SISO Coupled Tank System,” International Journal of Advanced Computer Science and Applications, vol. 12, no. 1, 2021. [Online]. Available: http://dx.doi.org/10.14569/IJACSA.2021.0120123 [16] P. Teppa,
M. Bravo, and G. Garcia, “Control por rechazo activo de perturbaciones del
nivel de líquido de un sistema de tanques acoplado,” Revista Faraute de
Ciencia y Tecnología, vol. 7, no. 1, pp. 10–18, 2012. [Online]. Available: https://upsalesiana.ec/ing33ar2r16
[17] P. Teppa Garran and G. Garcia, “Design of an optimal pid controller for a coupled tanks system employing adrc,” IEEE Latin America Transactions, vol. 15, no. 2,
pp. 189–196, 2017. [Online]. Available:
https://doi.org/10.1109/TLA.2017.7854611 |
|
[18] P. Teppa Garran, M. Faggioni, and G.
Garcia, “Optimal tracking in two-degree-of-freedom control systems: Coupled
tank system,” Journal of Applied Research and Technology, vol. 21, no. 4, pp.
560–570, 2023. [Online]. Available: https://doi.org/10.22201/icat.24486736e.2023.21.4.2000 [19] W. J. Rugh and J. S. Shamma, “Research on gain scheduling,” Automatica, vol. 36, no. 10, pp. 1401–1425, 2000.
[Online]. Available: https://doi.org/10.1016/S0005-1098(00)00058-3 [20] D. Rotondo, Advances in Gain-Scheduling and Fault Tolerant
Control Techniques. Springer Cham, 2018. [Online]. Available:
https://doi.org/10.1007/978-3-319-62902-5 [21] G. S. X. Bombois, D. Ghosh and J. Huillery, “Lpv system
identification for control using the local approach,” International Journal
of Control, vol. 94, no. 2, pp. 390–410, 2021. [Online]. Available:
https://doi.org/10.1080/00207179.2019.1596316 [22] Z. GAO and J. FU, “Robust lpv modeling
and control of aircraft flying through wind disturbance,” Chinese Journal of
Aeronautics, vol. 32, no. 7, pp. 1588–1602, 2019. [Online]. Available:
https://doi.org/10.1016/j.cja.2019.03.029 [23] S. Li, A.-T. Nguyen, T.-M. Guerra, and A. Kruszewski,
“Reduced-order model based Dynamic tracking for soft manipulators:
Data-driven lpv modeling, control design and
experimental results,” Control Engineering Practice, vol. 138, p. 105618,
2023. [Online]. Available: https://doi.org/10.1016/j.conengprac.2023.105618 [24] R. Robles, A. Sala, and M.
Bernal, “Performanceoriented quasi-lpv modeling of nonlinear systems,” International Journal
of Robust and Nonlinear Control, vol. 29, no. 5, pp. 1230–1248, 2019.
[Online]. Available: https://doi.org/10.1002/rnc.4444 [25] P. Persson and K. Astrom, “Dominant pole design - a unified view
of pid controller tuning,” IFAC Proceedings
Volumes, vol. 25, no. 14, pp. 377–382, 1992. [Online]. Available:
https://doi.org/10.1016/S1474-6670(17)50763-6 [26] A. D. Mammadov, E. Dincel, and M. T.
Söylemez, “Analytical design of discrete pi–pr controllers via dominant pole
assignment,” ISA Transactions, vol. 123, pp. 312–322, 2022. [Online].
Available: https://doi.org/10.1016/j.isatra.2021.05.038 [27] P. Teppa-Garrán and J. Andrade-Da
Silva, “An analytical interpolation approach for gain scheduling control of
linear parameter varying systems,” Ciencia e Ingeniería,
vol. 30, no. 1, pp. 93–101, 2008. [Online]. Available:
https://upsalesiana.ec/ing33ar2r27 |
[28] W. Tan, A. Packard, and G. Balas, “Quasi-lpv
modeling and lpv control of a generic missile,” in
Proceedings of the 2000 American Control Conference. ACC (IEEE Cat.
No.00CH36334), vol. 5, 2000, pp. 3692–3696. [Online]. Available:
https://doi.org/10.1109/ACC.2000.879259
[29] G. Vinco, S. Theodoulis, O. Sename, and G. Strub, “Quasi-lpv
modeling of guided projectile pitch dynamics through state transformation
technique,” IFAC-PapersOnLine, vol. 55, no. 35, pp.
43–48, 2022, 5th IFAC Workshop on Linear Parameter Varying Systems LPVS 2022.
[Online]. Available: https://doi.org/10.1016/j.ifacol.2022.11.288 [30] Z. He and L. Zhao, “Quadrotor trajectory tracking based on quasi-lpv system and internal model control,” Mathematical
Problems in Engineering, vol. 2015, no. 1, p. 857291, 2015. [Online].
Available: https://doi.org/10.1155/2015/857291 [31] P. S. Cisneros, A. Sridharan, and H. Werner, “Constrained
predictive control of a robotic manipulator using quasi-lpv
representations,” IFAC-PapersOnLine, vol. 51, no.
26, pp. 118–123, 2018, 2nd IFAC Workshop on Linear Parameter Varying Systems
LPVS 2018. [Online]. Available: https://doi.org/10.1016/j.ifacol.2018.11.158 [32] H. Xie, L. Dai, Y. Lu, and Y. Xia, “Disturbance rejection mpc framework for inputaffine
nonlinear systems,” IEEE Transactions on Automatic Control, vol. 67, no. 12,
pp. 6595–6610, 2022. [Online]. Available:
https://doi.org/10.1109/TAC.2021.3133376 33] J. Stefanovski, “Feedback affinization of nonlinear control
systems,” Systems & Control Letters, vol. 46, no. 3, pp. 207–217, 2002.
[Online]. Available: https://doi.org/10.1016/S0167-6911(02)00136-6 [34] J. Apkarian, Coupled water tank experiments manual. Quanser Consulting Advanced Teaching Systems, 1999.
[Online]. Available: https://upsalesiana.ec/ing33ar2r34 [35] R. C. Dorf and R. H. Bishop, Modern Control Systems. Prentice
Hall, 2008. [Online]. Available: https://upsalesiana.ec/ing33ar2r35 [36] A. Bartlett, C. Hollot, and H. Lin,
“Root locations of an entire polytope of polynomials: It suffices to check
the edges,” in 1987 American Control Conference, 1987, pp. 1611–1616.
[Online]. Available: https://doi.org/10.23919/ACC.1987.4789571 |