|
Scientific Paper / Artículo Científico |
|
|
|
|
https://doi.org/10.17163/ings.n33.2025.05 |
|
|
|
pISSN: 1390-650X / eISSN: 1390-860X |
|
|
CONTACT PATCHES OF RADIAL TIRES WITH DIFFERENT LENGTH-TO-WIDTH RATIOSUNDER STATIC LOADS |
||
|
PARCHES DE CONTACTO DE NEUMÁTICOS RADIALES CON DIFERENTES RELACIONES DE LONGITUD Y ANCHURA BAJO CARGA ESTÁTICA |
||
|
Received: 26-01-2024, Received after review: 09-10-2024, Accepted: 05-11-2024, Published: 01-01-2025 |
|
Abstract |
Resumen |
|
The aspect ratio of tires significantly influences the tread contact patch, which is closely related to the vehicle’s driving performance and handling. This study investigates the effect of radial tires with varying aspect ratios on contact patches under different loads and inflation pressures. The size and shape of the contact patches, along with the pressure distribution in tires with different aspect ratios, were analyzed. Five finite element tire models with aspect ratios of 55%, 60%, 65%, 70%, and 75% were developed. The simulation models of 205/55R16 were validated against experimental results. The findings reveal that as the aspect ratio increases, the contact length along the tire’s axial direction decreases, while the contact width along the rolling direction increases. Minimal differences in contact area were observed among tires with different aspect ratios under the same static load. For a given load, as the length-to-width ratio increases, the tread width of the contact patch decreases, while its length increases. Additionally, with an increasing length-to-width ratio, the contact patch shape transitions from a saddle to a barrel-like form. The maximum normal contact stress occurs at the shoulder of the tire for aspect ratios of 55%, 60%, and 65%, but shifts to the center of the tread for aspect ratios of 70% and 75%. The primary influence of the aspect ratio is on the contact size. |
La relación de aspecto de los neumáticos influye significativamente en el área de contacto de la banda de rodadura, afectando el rendimiento de conducción y manejo del vehículo. Este estudio analiza el efecto de neumáticos radiales con diferentes relaciones de longitud y diámetro en las manchas de contacto bajo diversas cargas o presiones de inflado. Se evaluaron el tamaño, forma y distribución de presión en neumáticos con relaciones de aspecto de 55 %, 60 %, 65 %, 70 % y 75 %, mediante cinco modelos de elementos finitos. El modelo 205/55R16 fue validado experimentalmente. Los resultados indican que, al aumentar la relación de aspecto, la longitud de contacto a lo largo del eje del neumático disminuye, mientras que la anchura en la dirección de rodadura aumenta. Bajo la misma carga estática, el área de contacto varía poco entre relaciones de aspecto diferentes. Sin embargo, con mayor relación longitud-anchura, el ancho de la banda de rodadura disminuye y la longitud aumenta. Asimismo, la forma de la mancha de contacto cambia de silla de montar a tambor de cintura. Los máximos valores de tensión de contacto normal se localizan en los hombros para relaciones de aspecto de 55 %, 60 % y 65 %, y en el centro de la banda para relaciones de 70 % y 75 %. La principal influencia de la relación de aspecto radica en el tamaño del contacto. |
|
Keywords: Aspect ratio, Contact patches, Contact stress, Radial tires |
Palabras clave: relación vertical y horizontal, parches de contacto, tensión de contacto, neumáticos radiales |
|
1Shanghai First Branch, Hua Yu Automotive Systems Co., LTD.,China. 2,*School of Automobile Engineering, Harbin Institute of Technology, Weihai, China. Corresponding author ✉: shenzj@hitwh.edu.cn. 3Process Technology Department, Guangxi Yuchai Machinery CO.,LTD., China.
Suggested citation: Qiao, F., Shen, Z. and Kang, Y. “Contact patches of radial tires with different length-towidth ratiosunder static loads,” Ingenius, Revista de Ciencia y Tecnología, N.◦ 33, pp. 49-59, 2025, doi: https://doi.org/10.17163/ings.n33.2025.05. |
|
1. Introduction
Tires are the only components of a vehicle that directly contact the road. They convert torque into force at the contact patch, enabling vehicle motion and significantly influencing driving and handling performance [1, 2]. The tire’s contact patch, which is closely associated with rolling resistance [3,4], directly impacts energy losses, fuel consumption, greenhouse gas emissions, and tread durability. Consequently, the grounding performance of tires has been extensively studied, with particular focus on the size and shape of the tire-road contact patch [5–9]. The finite element (FE) method and advanced experimental techniques have been widely employed to analyze tire grounding performance [10–13]. Guo et al. improved the UniTire side force model [14], demonstrating that the contact patch plays a critical role in cornering stiffness and lateral relaxation length. Patrick et al. [15] developed a 3D brush model to characterize contact patch size and pressure distribution. Alobaid et al. [16] enhanced an in-plane rigid-elastic-coupled tire model by incorporating the wheel’s vertical movement as a rigid body. This model connects road irregularities as input to the contact patch and outputs the wheel’s vertical motion. Additionally, Fathi et al. [17] established a tire finite element model using the Arbitrary Lagrangian-Eulerian formulation for steady-state analysis. However, these models often require substantial computational resources and numerous parameter assumptions, presenting challenges for practical applications. To validate the simulation results, pressure measurement film systems [18–22] have been developed to capture ground pressure distribution at the tireroad interface and analyze the relationships between imprint geometry characteristics and tread wear. Additionally, computer vision techniques and laser tire sensors have been employed to more accurately measure contact patches and tire deflection [23, 24]. Tomaraee et al. [25] utilized a well-equipped single-wheel tester to examine the relationship between imprint size, load, and inflation pressure. Swami et al. [26] developed a Stereo-Digital Image Correlation (DIC) application to generate three-dimensional (3D) visualizations of contact patches and extract dimensional information. Xie et al. [27] established a 3D finite element (FE) tire-pavement model to study the influence of bias-ply and radial tires on contact stress distribution. Their results demonstrated that the maximum contact stress between a radial tire and the road surface exceeds that of a bias-ply tire. Wang et al. [28] analyzed the effect of friction coefficient on horizontal contact stress using an improved simulation model that incorporates a neo-Hookean rubber material and a multilayer pavement structure. Oubahdou et al. [29] examined tire-pavement contact by employing a realistic |
description of normal sections and bends, providing detailed analyses of contact patch shape, stress distribution, and surface shear stresses at the tire-pavement interface. Jaime et al. [30] investigated the influence of pavement stiffness on 3D contact stress using a validated FE model. Their findings indicated that while pavement stiffness minimally affects normal contact stress, it significantly impacts longitudinal contact stress. Using a nonlinear FE tire model, Liu et al. [31] developed a tool for fast and accurate prediction of non-uniform tire-pavement contact stresses, integrating deep learning techniques. Relationships between wheel loading and contact patch behavior have been widely explored [32–34]. Zhang et al. [35] constructed a contact model for patterned tireasphalt pavement, analyzing contact behavior under static load and ABS conditions. Their results revealed that the contact area during braking is 7.7% smaller than that under static loading. Comparisons of contact pressure distributions under static and rolling conditions using FE tire models have shown that braking, acceleration, and cornering significantly impact contact stress distributions, with contact patch length increasing as tire speed decreases [36,37]. Gu et al. [38] concluded that the longitudinal contact patch length decreases with higher inflation pressure. The contact patch width must be considered for lateral stress analysis [39]. The contact patch plays a crucial role in tire performance, influencing tread wear, steering responsiveness, wet and dry handling, traction, tire noise, and ride quality. Therefore, investigating the tire contact patch is essential for optimizing tire performance. Among the factors affecting the contact patch, the tire aspect ratio is a significant contributor. However, limited studies have explored the relationship between the tire aspect ratio and the contact patch. This study aims to examine the effects of tire aspect ratio on the contact patch under various vertical load and inflation pressure conditions. Finite element (FE) models of the 205/55R16 tire were developed using ABAQUS 6.14 and validated by comparing simulation results of load and deflection with experimental data. Additional FE tire models with aspect ratios of 55%, 60%, 65%, 70%, and 75% were also established. The study analyzed the imprint shapes and contact stress distributions across different vertical loads and inflation pressures. The article is structured as follows: it begins with a description of the tire materials and modeling process, followed by the validation of the FE models. The discussion section then explores the relationship between tire aspect ratio and the contact patch under static conditions.
|
|
2. Materials and methods
The finite element (FE) model and cross-section of the 205/55R16 tire are illustrated in Figure 1. The width of the tire’s cross-section is 205 mm, with an aspect ratio (height-to-width) of 55%. The rim diameter measures 406.4 mm, and the wheel radius is 315.95 mm. Additional FE models with aspect ratios of 60%, 65%, 70%, and 75% were developed by adjusting the cross-section width while maintaining the tire height constant.
Figure 1. Simulation model of tire 205/55R16
The pavement and rim were simplified as rigid surfaces since their stiffness is significantly higher than that of the tire. To ensure higher mesh quality, only the longitudinal tread pattern was considered in the tire model, while the transverse tread pattern was omitted. The two-dimensional cross-sections of the tire were created using AutoCAD software and subsequently imported into ABAQUS to develop the 3D models. Two belts were incorporated into the simulation: Belt 1, located closer to the tread, had a width of 94 mm, while Belt 2 had a width of 114 mm. A concentrated force along the Z-axis was applied at the center point of the rim. The discretization method for tire-pavement interaction was utilized to predict surface-to-surface contact. A penalty function was employed to simulate tangential contact behavior, with a friction coefficient set at 0.8. Additionally, the grounding mesh was refined to enhance the accuracy of the modeling predictions. The hyperelastic mechanical properties of rubber materials are described using the Mooney-Rivlin constitutive model [40]. The corresponding material properties are provided in Table 1. In this study, rubber deformation is modeled as uniform deformation of isotropic hyperelastic bodies. Consequently, the strain energy density is expressed using strain invariants as follows:
Table 1. Mooney-Rivlin material properties
|
Where I3 = 1 Given that the material is fully incompressible, equation (1) simplifies to:
Where, Cij represent the material coefficients. For practical engineering applications, equation (2) is further reduced to:
The rubber-cord composite was simulated using rebar elements to account for both rubber and cord materials simultaneously, with each material meshed separately. The properties of the rebar material are listed in Table 2. Inflation pressure was applied to the inner surface of the tire to simulate various inflation conditions. According to the GB/T 2977-2016 standard, the parameters of the tire are defined as: Where, B is the designed tire section width, B* is the inflated tire section width, H is the section height, D is the rim diameter, D* is the inflated tire diameter.
Table 2. Rebar material properties
2.1.Model validation
To validate the model, the relationship between tire deflection and static load was compared with experimental data from reference [41]. The experiments were conducted using a 5-in-1 Tire Stiffness Testing Machine (ke · TEK, Taiwan Hung Ta Instrument Co., Ltd) with a maximum displacement of 1500 mm and an accuracy of ± 0.1 mm. The tested tire was a 205/55 R16, with a tire pressure of 0.24 MPa. Radial loads of 3000 N, 3500 N, 4000 N, and 5000 N were applied. The same parameters were used in the finite element (FE) simulations. The largest error between the simulation and experimental results was 6.8%, indicating that the simplified FE tire model is reasonable and suitable for investigating the relationship between aspect ratio and tire-ground contact patch. Simulation and experimental results for deflection under different static loads are presented in Table 3. |
|
Table 3. Simulation and experimental results with relative error
|
3. Results and Discussion
3.1.The size and shape of the contact patch under varying vertical loads
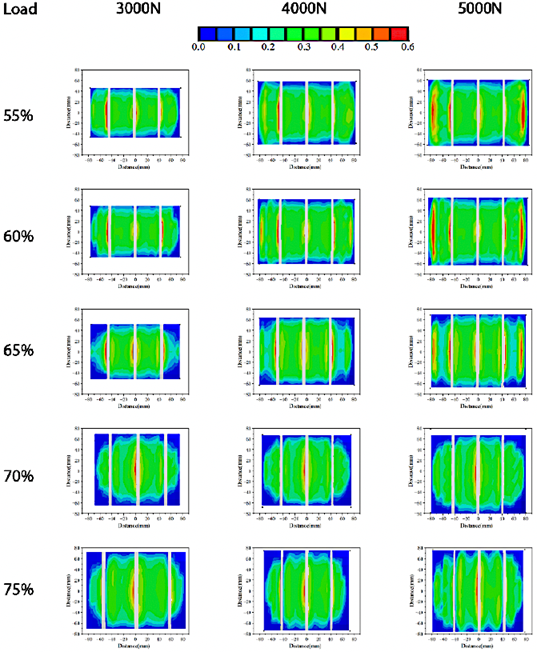
Figure 2 illustrates the contact patches of tires with varying aspect ratios under vertical loads of 3000 N, 4000 N, and 5000 N. |
|
Figure 2. The shape of the contact patches of tires with different aspect ratios under varying vertical loads |
|
The inflation pressure was set to 0.24 MPa. Figure 2 shows that the contact patch exhibited a saddle shape for aspect ratios of 55% and 60%, transitioned to a rectangular shape for an aspect ratio of 65%, and evolved into a waist-drum shape for aspect ratios of 70% and 75%. To better characterize the contact patch, the tread contact length and width were measured. The tread contact length refers to the maximum length of the contact patch along the tire’s rolling direction, while the tread contact width represents the maximum width of the contact patch along the tire’s axial direction. The contact areas for different aspect ratios, obtained from ABAQUS simulations, are presented in Table 4. The results indicate that as the aspect ratio increases, the tread contact width decreases, while the tread contact length increases under the same static load. Additionally, for a given aspect ratio, both the tread contact width and length, as well as the overall contact patch area, increase with higher vertical loads.
Table 4. The size of the contact patch of tires with different aspect ratios under different vertical loads
Figure 3 illustrates the relationships between the aspect ratio and the contact patch area under varying vertical loads. The results indicate that the contact patch area increases as the vertical load increases. Under loads of 3000 N and 4000 N, the contact patch area fluctuates with increasing aspect ratio, whereas under a load of 5000 N, it consistently increases with higher aspect ratios. The relationship between the tire aspect ratio and the contact patch area is non-linear. A larger contact patch area generally results in reduced vibration and noise, as well as improved grip performance. However, an increased contact patch area also leads to higher average tread wear and greater energy loss. Across all three vertical loads, the tire with an aspect ratio of 55% exhibited a relatively smaller contact area. |
Figure 3. Relation curves between the aspect ratio and the contact patch area under different loads
3.2.Contact stress distribution under different vertical loads
Figure 4 presents the contact stress distribution of tires along the node path for different aspect ratios under varying vertical loads.
Figure 4. Contact stress distribution of tires with different aspect ratios under different loads |
|
The contact stress curves along the tread width exhibit a multi-peak pattern, with peak values primarily concentrated at the shoulder and longitudinal groove. This pattern arises from stress concentrations caused by abrupt changes in tread geometry at the shoulder and longitudinal groove. It was due to stress concentration caused by dramatic changes in tread shape at the shoulder and groove. For the vertical load of 3000N as shown in Figure 4a, the peak value of contact stress was mainly distributed in the tread groove, and the peak values of tire with aspect ratio of 60% and 65% were larger than that of other aspect ratio tires. For the vertical load of 4000N as shown in Figure 4b, the contact stress increased obviously at the shoulder. The maximum contact stress was at the shoulder of the tire with aspect ratio of 60%. For a vertical load of 5000N, as shown in Figure 4c, the contact stress on both sides of the tread decreased with an increase in the aspect ratio, while the contact stress at the center of the tread increased. The maximum contact stress was observed at the shoulder of the tire for aspect ratios of 55%, 60%, and 65%. In contrast, for aspect ratios of 70% and 75%, the maximum stress shifted to the central part of the tread. Regions with |
higher contact stress typically experience more severe wear [42]. Additionally, as the center of the tread is thinner, aspect ratios of 70% and 75% may reduce the tire’s service life.
3.3.Size and shape of the contact patch under different inflation pressures
The sizes of the contact patches for tires under varying inflation pressures are presented in Table 5. The width of the contact patch decreased progressively as the aspect ratio increased, while the length of the contact patch increased under the same inflation pressure. Both the width and length of the contact patch, as well as its overall area, decreased with increasing inflation pressure for a given aspect ratio. Figure 5 illustrates the contact patches of tires with different aspect ratios under inflation pressures of 0.20, 0.24, and 0.28 MPa. The vertical load was set at 3000 N. The results show that the shape of the contact patch transitioned from a saddle shape to a waist drum shape as the aspect ratio increased under the same inflation pressure. Additionally, as the inflation pressure increased, the distribution of contact stress became more uneven. |
|
Figure 5. Contact patch shapes of tires with varying aspect ratios under different inflation pressures |
|
Table 5. Size of the contact patch for tires with different aspect ratios under various inflation pressures
Figure 6 illustrates the relationship between the aspect ratio and the contact patch area under various inflation pressures. The data reveal that the contact patch area decreases as inflation pressure increases. At an inflation pressure of 0.2 MPa, the contact patch area increases as the aspect ratio rises from 60% to 70%. For an inflation pressure of 0.24 MPa, the contact patch area fluctuates with increasing aspect ratio. Conversely, at an inflation pressure of 0.28 MPa, the contact patch area decreases as the aspect ratio increases. Across all three inflation pressure conditions, tires with an aspect ratio of 55% consistently exhibited relatively smaller contact patch areas.
Figure 6. Relation curves between aspect ratio and contact patch area under different inflation pressures
3.4.Contact stress distribution under different inflation pressures
Contact pressure is a critical factor in vehicle performance, directly influencing grip and traction. These parameters are closely associated with a vehicle’s acceleration, braking, and cornering capabilities. While higher contact pressure generally enhances grip, excessive pressure can accelerate tire wear prematurely. |
Figure 7 illustrates the contact stress distribution of tires along the node path for different aspect ratios under varying inflation pressures. The contact stress curves along the tread width exhibited a multi-peak pattern. As inflation pressure increased, contact stress at the shoulders decreased, while stress at the longitudinal grooves increased. When inflation pressure was set to 0.20 MPa (Figure 7a), the peak contact stress remained below 0.6 MPa. In contrast, at inflation pressures of 0.24 MPa and 0.28 MPa (Figures 7b and 7c), the peak contact stress exceeded 0.6 MPa. Across all inflation pressures, the peak contact stress at the grooves on both sides of the tread for tires with aspect ratios of 60% and 65% was higher than those of other aspect ratios. Conversely, the contact stress at the middle groove of the tread for aspect ratios of 60% and 65% was lower than those observed in other aspect ratios under identical inflation conditions.
Figure 7. Contact stress distribution of tires with different aspect ratios under varying inflation pressures
|
|
Uneven contact pressure distribution leads to irregular tire wear. As shown in Figure 7a, tires with aspect ratios of 70% and 75% exhibit lower and more uniform contact stress compared to those with aspect ratios of 55%, 60%, and 65%. This suggests a higher likelihood of uneven wear for tires with lower aspect ratios. When inflation pressure increased from 0.2 MPa to 0.24 Mpa (Figure 7b), this disparity became more pronounced. Additionally, the contact stress at the shoulder of tires with lower aspect ratios is higher than that of tires with higher aspect ratios, indicating better stability and handling during cornering. The contact stress at the center of the tread is nearly identical across all aspect ratios, with the primary differences occurring at the shoulder and longitudinal grooves.
4. Conclusions
This study presents finite element (FE) models of 205/XX R16 tires developed using ABAQUS software to investigate the size and shape of the contact patch, as well as the axial distribution of contact pressure within the contact patch for tires with different aspect ratios under varying static wheel loads and inflation pressures. The main conclusions are as follows:
1. The FE simulation results for tire deflection under different static loads align closely with experimental data, with a maximum error of 6.8%, confirming the accuracy and reliability of the model. 2. The tread width of the contact patch decreased, and the length increased as the aspect ratio increased. The contact patch area fluctuated with increasing aspect ratio under static loads of 3000 N and 4000 N, while it increased consistently under a static load of 5000 N. The shape of the contact patch evolved from a saddle shape to a waist-drum shape as the aspect ratio increased. 3. Lower inflation pressures resulted in larger contact patch areas and a more uniform distribution of contact stress. As inflation pressure increased under the same static wheel load, the contact stress at the center of the tread increased. 4. The contact stress distribution along the axial direction of the tire exhibited a multi-peak pattern, with peaks primarily located at the shoulder and longitudinal grooves. For tires with aspect ratios of 55%, 60%, and 65%, the maximum contact stress was observed at the shoulder. In contrast, for tires with aspect ratios of 70% and 75%, the maximum stress occurred at the center of the tread. |
References
[1] M. Abe, Vehicle Handling Dynamics (Second Edition, second edition ed., M. Abe, Ed. Butterworth-Heinemann, 2015. [Online]. Available: https://doi.org/10.1016/B978-0-08-100390-9.01001-0 [2] Y. Suo, W. Yang, D. Lu, Y. Zhang, and M. Che, “Analysis of camber-caused asymmetric characteristics using finite element method and pure camber semi-empirical modeling,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, p. 09544070241272802, 2024. [Online]. Available: https://doi.org/10.1177/09544070241272802 [3] F. B. Luigi Romano and B. Jacobson, “An extended lugre-brush tyre model for large camber angles and turning speeds,” Vehicle System Dynamics, vol. 61, no. 6, pp. 1674–1706, 2023. [Online]. Available: https://doi.org/10.1080/00423114.2022.2086887 [4] Z. Shi, Y. M. Mohammed, N. Uddin, and G. Chen, “A vehicle-bridge interaction model considering contact patch size and vehicle self-generated excitation – a theoretical study,” Engineering Structures, vol. 298, p. 117079, 2024. [Online]. Available: https://doi.org/10.1016/j.engstruct.2023.117079 [5] C. Suvanjumrat and J. Phromjan, “The contact patch characterization of various solid tire testing methods by finite element analysis and experiment,” International Journal of Geomate, vol. 19, no. 76, pp. 25–32, 2020. [Online]. Available: https://doi.org/10.21660/2020.76.9134 [6] N. Ryzí, R. StoÄ ek, J. Maloch, and M. StÄ›niÄ ka, “How does heat generation affect the cut and chip wear of rubber?” Polymer Bulletin, vol. 81, no. 18, pp. 17 213–17 232, Dec 2024. [Online]. Available: https://doi.org/10.1007/s00289-024-05498-1 [7] Y. Nakajima and S. Hidano, “Theoretical tire model considering two-dimensional contact patch for force and moment,” Tire Science and Technology, vol. 50, no. 1, pp. 27–60, 07 2021. [Online]. Available: https://doi.org/10.2346/tire.21.20005 [8] J. Prakash, M. Vignati, and E. Sabbioni, “An exponential decay model for decaying of contact patch friction steering moment with rolling speed,” Tire Science and Technology, vol. 52, no. 1, pp. 34–50, 03 2024. [Online]. Available: https://doi.org/10.2346/tire.23.21017 [9] J. Bastiaan, A. Chawan, W. Eum, K. Alipour, F. Rouhollahi, M. Behroozi, and J. Baqersad, “Intelligent tire prototype in longitudinal slip operating conditions,” Sensors, vol. 24, no. 9, 2024. [Online]. Available: https://doi.org/10.3390/s24092681 |
|
[10] J. M. Conradie, P. S. Els, and P. S. Heyns, “Finite element modelling of off-road tyres for radial tyre model parameterization,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, vol. 230, no. 4, pp. 564–578, 2016. [Online]. Available: https://doi.org/10.1177/0954407015590018 [11] M. Zhang, H.-J. Unrau, M. Gießler, and F. Gauterin, “A detailed tire tread friction model considering dynamic friction states,” Tribology International, vol. 193, p. 109342, 2024. [Online]. Available: https://doi.org/10.1016/j.triboint.2024.109342 [12] Z. Liu, F. Wang, Z. Cai, Y. Wei, and S. Marburg, “A novel theoretical model of tire in-plane dynamics on uneven roads and its experimental validation,” Mechanical Systems and Signal Processing, vol. 186, p. 109854, 2023. [Online]. Available: https://doi.org/10.1016/j.ymssp.2022.109854 [13] P. Millan and J. Ambrósio, “Tire–road contact modelling for multibody simulations with regularised road and enhanced ua tire models,” Multibody System Dynamics, Apr 2024. [Online]. Available: https://doi.org/10.1007/s11044-024-09987-z [14] Guo, Konghui, Chen, Ping, Xu, Nan, Yang, Chao, and Li, Fei, “Tire side force characteristics with the coupling effect of vertical load and inflation pressure,” SAE International Journal of Vehicle Dynamics, Stability, and NVH, vol. 3, no. 1, pp. 19–30, nov 2018. [Online]. Available: https://doi.org/10.4271/10-03-01-0002 [15] P. Riehm, H.-J. Unrau, F. Gauterin, S. Torbrügge, and B. Wies, “3d brush model to predict longitudinal tyre characteristics,” Vehicle System Dynamics, vol. 57, no. 1, pp. 17–43, 2019. [Online]. Available: https://doi.org/10.1080/00423114.2018.1447135 [16] F. Alobaid and S. Taheri, “The modified in-plane rigid-elastic-coupled tire modal model: dynamic response to short wavelength road profiles,” Vehicle System Dynamics, vol. 62, no. 12, pp. 3076–3097, 2024. [Online]. Available: https://doi.org/10.1080/00423114.2024.2316683 [17] H. Fathi, Z. El-Sayegh, and M. H. R. Ghoreishy, “Prediction of rolling resistance and wheel force for a passenger car tire: A comparative study on the use of different material models and numerical approaches,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, p. 09544070241244556, 2024. [Online]. Available: https://doi.org/10.1177/09544070241244556 |
[18] X. Gao, Y. Wang, W. Fan, Z. Long, X. Li, X. Yue, Y. Liu, Y. Yan, and J. Wang, “Modeling and experimental verification of torsional deformation constitutive model of tread rubber based on digital image correlation,” Experimental Techniques, vol. 47, no. 4, pp. 749–765, Aug 2023. [Online]. Available: https://doi.org/10.1007/s40799-022-00583-4 [19] S. K. Pradhan, A. S. Rathore, S. Sehgal, P. Sonia, G. Ramu, and C. Prakash, “Development and validation of test rig for experimental analysis of contact behavior between rail wheel-rail and rubber tire-rail in road cum rail vehicles,” Indian Journal of Engineering and Materials Sciences (IJEMS), vol. 31, no. 1, pp. 84–92, 2024. [Online]. Available: https://doi.org/10.56042/ijems.v31i1.986 [20] J. Guan, X. Zhou, L. Liu, M. Ran, and Y. Yan, “Investigation of tri-axial stress sensing and measuring technology for tire-pavement contact surface,” Coatings, vol. 12, no. 4, 2022. [Online]. Available: https://doi.org/10.3390/coatings12040491 [21] T. Saisaengtham, J. Phromjan, R. Rugsaj, S. Phakdee, and C. Suvanjumrat, “Pavement-tire contact patch effects on air volume using finite element method,” International Journal of Geomate, vol. 26, no. 113, pp. 50–57, 2024. [Online]. Available: https://doi.org/10.21660/2024.113.g13179 [22] C. Liang, D. Zhu, G. Wang, and M. Shan, “Experimental study on tire-road dynamic contact pressure distribution using ftir imaging,” International Journal of Automotive Technology, vol. 22, no. 5, pp. 1305–1317, Oct 2021. [Online]. Available: https://doi.org/10.1007/s12239-021-0114-3 [23] N. Xu, H. Askari, Y. Huang, J. Zhou, and A. Khajepour, “Tire force estimation in intelligent tires using machine learning,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 4, pp. 3565–3574, 2022. [Online]. Available: https://doi.org/10.1109/TITS.2020.3038155 [24] N. Xu, J. Zhou, B. H. G. Barbosa, H. Askari, and A. Khajepour, “A soft sensor for estimating tire cornering properties for intelligent tires,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 53, no. 10, pp. 6056–6066, 2023. [Online]. Available: https://doi.org/10.1109/TSMC.2023.3281474 |
|
[25] P. Tomaraee, A. Mardani, A. Mohebbi, and H. Taghavifar, “Relationships among the contact patch length and width, the tire deflection and the rolling resistance of a free-running wheel in a soil bin facility,” Spanish Journal of Agricultural Research, vol. 13, no. 2, p. e0211, May 2015. [Online]. Available: https://doi.org/10.5424/sjar/2015132-5245 [26] A. Swami, C. Liu, J. Kubenz, G. Prokop, and A. K. Pandey, “Experimental study on tire contact patch characteristics for vehicle handling with enhanced optical measuring system,” SAE International Journal of Vehicle Dynamics Stability and NVH, vol. 5, no. 3, pp. 333–350, 2021. [Online]. Available: https://doi.org/10.4271/10-05-03-0023 [27] Y. Xie and Q. Yang, “Tyre–pavement contact stress distribution considering tyre types,” Road Materials and Pavement Design, vol. 20, no. 8, pp. 1899–1911, 2019. [Online]. Available: https://doi.org/10.1080/14680629.2018.1473285 [28] Y. Wang, Y. Lu, and C. Si, “Tirepavement coupling dynamic simulation under tire high-speed-rolling condition,” International Journal of Simulation Modelling, vol. 15, pp. 236–248, 06 2016. [Online]. Available: http://dx.doi.org/10.2507/IJSIMM15(2)4.332 [29] Y. Oubahdou, E.-R. Wallace, P. Reynaud, B. Picoux, J. Dopeux, C. Petit, and D. Nélias, “Effect of the tire – pavement contact at the surface layer when the tire is tilted in bend,” Construction and Building Materials, vol. 305, p. 124765, 2021. [Online]. Available: https://doi.org/10.1016/j.conbuildmat.2021.124765 [30] J. A. Hernandez and I. L. Al-Qadi, “Tire–pavement interaction modelling: hyperelastic tire and elastic pavement,” Road Materials and Pavement Design, vol. 18, no. 5, pp. 1067–1083, 2017. [Online]. Available: https://doi.org/10.1080/14680629.2016.1206485 [31] X. Liu and I. L. Al-Qadi, “Three-dimensional tire-pavement contact stresses prediction by deep learning approach,” International Journal of Pavement Engineering, vol. 23, no. 14, pp. 4991–5002, 2022. [Online]. Available: https://doi.org/10.1080/10298436.2021.1990288 [32] J. Ye, Z. Zhang, J. Jin, R. Su, and B. Huang, “Estimation of tire-road friction coefficient with adaptive tire stiffness based on rcsckf,” Nonlinear Dynamics, vol. 112, no. 2, pp. 945–960, Jan 2024. [Online]. Available: https://doi.org/10.1007/s11071-023-09088-0 |
[33] Sun, Lihong, Lu, Dang, and Li, Bing, “Analysis and prediction of tire traction properties for different inflation pressures based on vertical deflection control method,” SAE International Journal of Vehicle Dynamics, Stability, and NVH, vol. 5, no. 3, pp. 307–315, apr 2021. [Online]. Available: https://doi.org/10.4271/10-05-03-0021 [34] Z. Gong, Y. Miao, W. Li, W. Yu, and L. Wang, “Analysis of tyre-pavement contact behaviour of heavy truck in full-scale test,” International Journal of Pavement Engineering, vol. 24, no. 1, p. 2235630, 2023. [Online]. Available: https://doi.org/10.1080/10298436.2023.2235630 [35] B. Zheng, J. Chen, R. Zhao, J. Tang, R. Tian, S. Zhu, and X. Huang, “Analysis of contact behaviour on patterned tire-asphalt pavement with 3-d fem contact model,” International Journal of Pavement Engineering, vol. 23, no. 2, pp. 171–186, 2022. [Online]. Available: https://doi.org/10.1080/10298436.2020.1736294 [36] S. T. Pooya Behroozinia and R. Mirzaeifar, “An investigation of intelligent tires using multiscale modeling of cord-rubber composites,” Mechanics Based Design of Structures and Machines, vol. 46, no. 2, pp. 168–183, 2018. [Online]. Available: https://doi.org/10.1080/15397734.2017.1321488 [37] I. L. A.-Q. Hao Wang and I. Stanciulescu, “Simulation of tyre–pavement interaction for predicting contact stresses at static and various rolling conditions,” International Journal of Pavement Engineering, vol. 13, no. 4, pp. 310–321, 2012. [Online]. Available: https://doi.org/10.1080/10298436.2011.565767 [38] T. Gu, B. Li, Z. Quan, S. Bei, G. Yin, J. Guo, X. Zhou, and X. Han, “The vertical force estimation algorithm based on smart tire technology,” World Electric Vehicle Journal, vol. 13, no. 6, 2022. [Online]. Available: https://doi.org/10.3390/wevj13060104 [39] P. Rosca, M. L. Marmureanu, T. V. Tiganescu, C. M. Pîrvulescu, I. M. Bîndac, and C. Doru, “Determination of tyre-ground interaction parameters through image processing in matlab,” International Journal of Heavy Vehicle Systems, vol. 28, no. 5, pp. 630–649, 2021. [Online]. Available: https://doi.org/10.1504/IJHVS.2021.120913 [40] H. B. Huang, X. D. Yu, J. P. Liu, and Z. Yao, “Asymmetry investigation on radial tire contact pressure distribution,” Chinese Journal of System Simulation, vol. 30, no. 8, pp. 2991–2998, 2018. [Online]. Available: https://doi.org/10.16182/j.issn1004731x.joss.201808021 |
|
[41] T. Doi and K. Ikeda, “Effect of tire tread pattern on groove wander of motorcycles,” Tire Science and Technology, vol. 13, no. 3, pp. 147–153, 07 1985. [Online]. Available: https://doi.org/10.2346/1.2150992
|
[42] C. Wang, H. Huang, X. Chen, and J. Liu, “The influence of the contact features on the tyre wear in steady-state conditions,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, vol. 231, no. 10, pp. 1326–1339, 2017. [Online]. Available: https://doi.org/10.1177/0954407016671462 |